我相信，许多朋友在学习时肯定会在主题列表上有数学。许多人不了解数学在哪里有趣的地方，数学的美丽在哪里？本文仔细选择了适合年轻人和老年人的10个算术问题，并导致每个人都以各种形式探索数学世界的角落，例如定理，有趣的问题甚至未解决的奥秘。许多问题都包含深刻的数学知识，它触及了数学的所有领域。我希望那些自童年时代以来数学失败的朋友都可以接受有趣的数学主题。

资料来源：Pixabay

数字黑洞6174

选择任何四位数的数字（数字不能相同），排列从大到小的所有数字，然后将所有数字从小到大的数字排列，然后从前者中减去后者以获取新的数字。在新获得的数字上重复上述操作，在7个步骤内，您将不可避免地获得6174。

例如，选择一个四位数的6767：

7766-6677=1089

9810-0189=9621

9621-1269=8352

8532-2358=6174

7641-1467=6174

.

6174“黑洞”称为Kaprekar常数。对于三位数，还有一个数字黑洞——495。

3x + 1问题

从任何正整数开始，重复以下操作：如果数字为偶数，则将其除以2；如果数字为奇数，则将其扩展到3次，然后添加1。您会发现该序列最终将成为4、2、1、4、2、1、5的周期。

例如，根据上述规则，所选的数字为67，您可以按顺序获得：

67、201、101、304、152、76、38、19、58、29、88、44、22、11、11、11、11、17,52、26、13、26、20、20、10、10、10、16、16、8、4、2、1、1、4、4、2、1、5

数学家尝试了很多数字，而且他们都无法逃脱“ 421陷阱”。但是，序列最终是否成为所有数字的4、2、1循环？

乍一看，这个问题可以说是一个“坑” .——，这个问题非常简单，有很多突破，因此数学家接一个地跳入它。但是，他们不知道很容易进出，而且许多数学家在死亡之前永远不会遇到这个问题。有无数的数学家被抓住了，可以从三个+1问题的各种别名中看出：3x+1问题也称为Collatz猜想，锡拉丘兹问题，Kakutani问题，Kakutani问题，Hasse算法，Hasse Algorithm，Ulam问题等。后来，由于对NAM的争议，因此无法从中受益。

到目前为止，数学家尚未证明该法律对所有数字都是正确的。

特殊两位数乘法的速度计算

如果两个两个两位数的数字是相同的，并且将单位数字添加到10位，则可以立即说出两个数字的乘积。如果这两个数字分别写为AB和AC，则其产品的前两个数字是A和A+1的产物，最后两个数字是B和C的乘积。

例如，十位数为47和43的数字相同，单位数字的总和为10，因此其产品的前两个数字为4（4+1）=20，而最后两个数字为73=21。也就是说，4743=2021。

同样，6169=4209，8684=7224，3535=1225，等。

这种快速计算方法背后的原因是（10x + y）（10x +（10 -y））=100 x（x + 1） + y（10 -y）对x和y都保留。

魔术广场上的魔术“正方形”

“三阶魔术平方”是指将数字1到9填充到33正方形中，以便每行，每列和两个对角线的三个数字的总和完全相同。下图是三阶魔术正方形，每条直线上的三个数字的总和等于15。

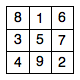
您可能听说过魔术广场，但您不知道魔术广场的一些奇妙特性。例如，任何三阶魔术方形平方都可以满足由每行组成的三位数数字的平方之和等于由每行反向顺序组成的三位数数字的平方之和。对于上图中的第三级魔术广场，有

816+357+492=618+753+294

使用线性代数，我们可以证明这一结论。

自然形成的魔术公式

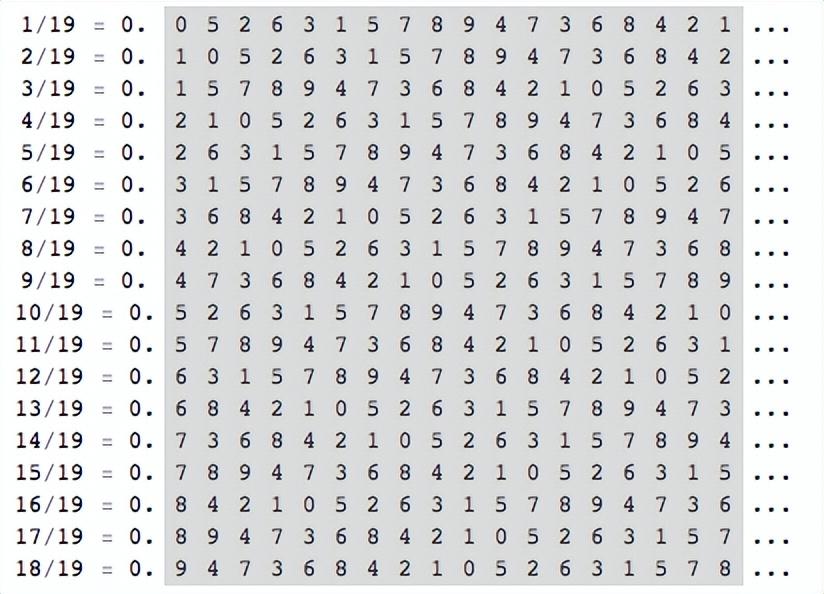
从1/19到18/19的18个分数的小数部分的长度是18。将这18个周期部分安排为1818的数字阵列，该阵列仅形成一个魔术广场——每行，列，两条对角线上的数字总和为81（注意：注意：严格地认为，它是一个魔术平方，因为它是一个方形的数字，因为有一个正方形的数字。

196算法

一个数字向前读和逆转是相同的，因此我们称其为“ palindrome”。选择任何数字，并在以相反的形式编写后继续添加您获得的数字，直到获得引导号码为止。例如，如果选定的数字为67，则可以在两个步骤中获得一个484：

67 + 76=143

143 + 341=484

将69个变成回文需要四个步骤：

69 + 96=165

165 + 561=726

726 + 627=1353

1353 + 3531=4884

89的“通往回教之路”特别长。在8813200023188步骤24之前，您将不会获得第一个回文编号。

每个人都可能认为，毫不奇怪的是，他们总是能够通过不断地添加“一个积极和一个反向”来获得许多回文。事实是真的。 ——。如果根据规则添加几乎所有数字，则迟早出现allindromes的数量。但是，196是一个相当引人注目的例外。数学家已经使用计算机来计算超过3亿位数字，但从未产生一次回文数。从196开始，我们可以添加全文的数量吗？ 196有什么特别之处？这仍然是一个谜。

Farey序列

选择一个正整数n。找出所有最简单的分数，不超过N，然后将它们从小到大的分类。该分数序列称为Farey序列。例如，以下是当n=7时的farey序列。

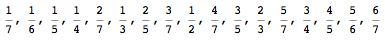
定理：在Farey序列中，对于任何两个相邻的分数，首先计算前者的分母并乘以后者的分子，然后计算前者的分子并乘以后者的分母，然后将两种产物乘以1个不同的1个不同！

该定理有各种各样的证据，从数字理论到图理论。甚至有一种方法可以借助选择定理将其转换为不言而喻的几何问题，从而巧妙地证明它！

唯一的解决方案

经典数字拼图：使用1到9形成一个九位数字，以便可以将该数字的第一个数字除以1，可以将前两个数字组成的两个数字除以2，而前三位数字组成的三位数可以将3位数字划分为3，直到整个Ninine Vigit数字可以划分为9。

没错，实际上有一个很大的数字：381654729。其中3个可以按1，38排除，38可以按2和381进行除外，直到381可以按3进行除外，直到可以通过分隔属性逐步逐步逐步得出整个数字，可以通过9个分步逐步派生，可以使用分隔属性使用计算机，也可以使用分隔计算机。

另一个有趣的事实是，在所有362,880个不同的九位数字中，由1到9，381654,729组成，是唯一满足要求的数字！

数字正在变化，数字保持不变

123456789的双重数为246913578，恰好是另一个由1到9组成的数字。

246913578的双重数为493827156，恰好是另一个由1到9组成的数字。

将493827156再次加倍987654312，它仍然恰好由数字1到9组成。

如果将987654312加倍，您将获得10位数字1975308624，该数字仍然没有重复的数字，并且恰好由10个数字0到9组成。

1975308624两倍，这个数字将成为3950617248，它仍然由0到9组成。

但是，该规则不会继续。继续加倍3950617248，除了第一个例外，您将获得7901234496。

三个神奇的分数

小数点分为两位数后，1/49等于0.0204081632。前五个数字依次为2、4、8、16、32，每个数字正好是上一个数字的两倍。

100/9899等于0.01010102030813213455 .在断开了两个数字之后，每个数字正好是前两个数字的总和（即FibonAcci序列）。

和100/9801等于0.0102030405070808091111121314151617181920212223 .

组合数学中的“生成函数”可以完美解释这些现象的原因。

资料来源该文章来自微信的公共帐户Guoke 2023-03-12 20:00在Sichuan中发布

语句文章中的图片，视频和内容均来自原始文章，钥匙共享，版权属于原始作者和原始来源。文章中的观点仅代表作者的个人观点。如果有任何侵权，请及时与我们联系，我们将及时纠正或删除。